

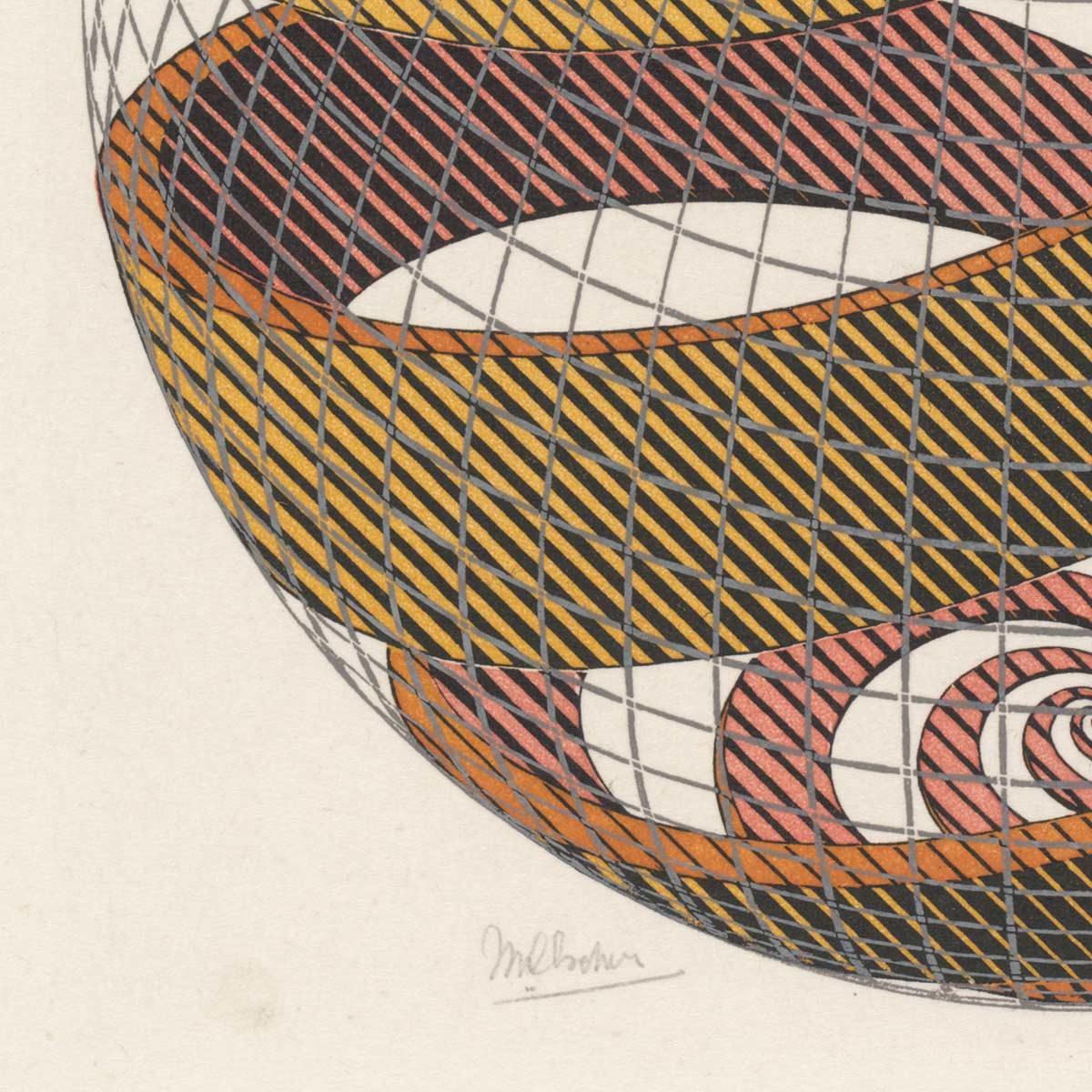
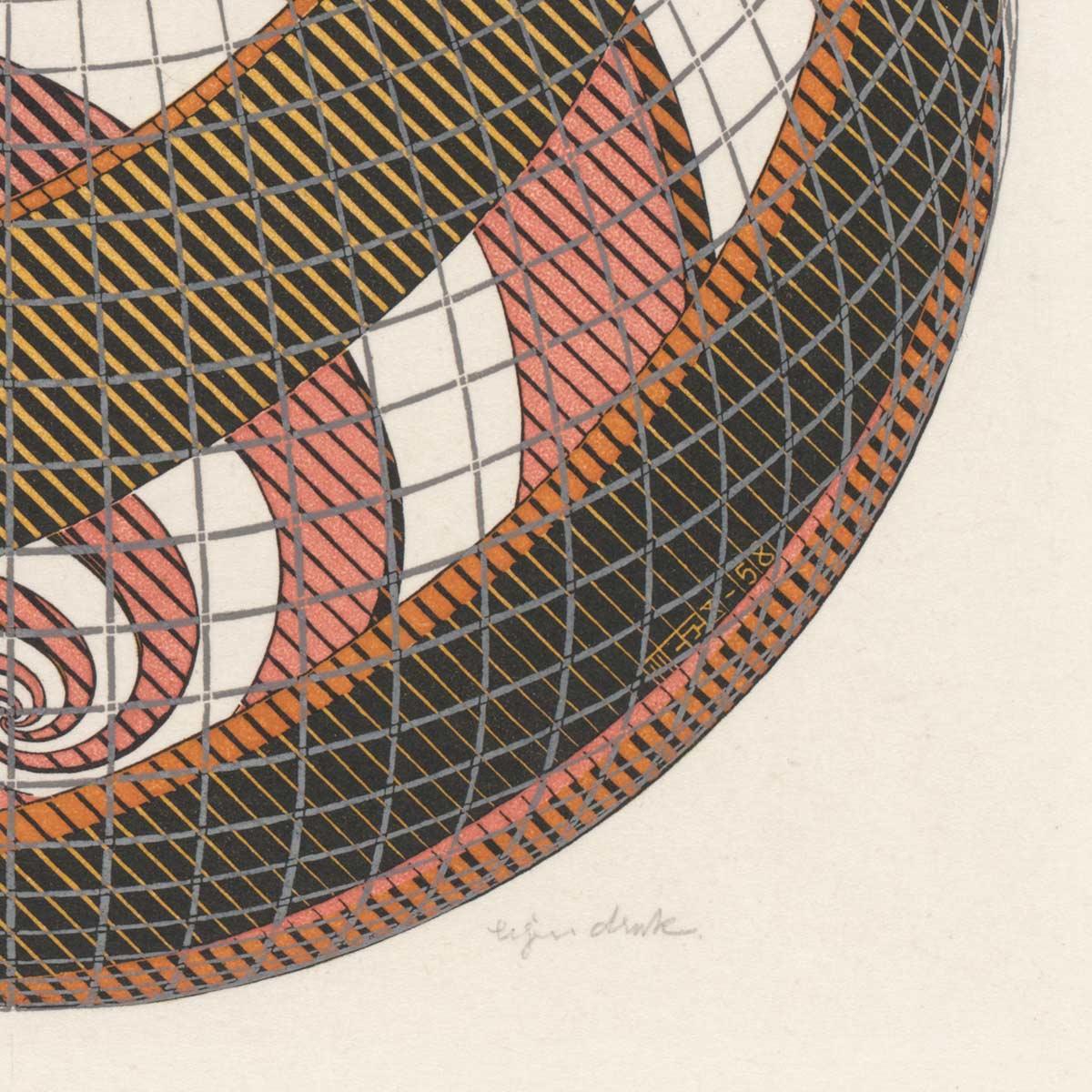
In October 1958, Escher created one of his most beautiful, but also most complex objects. He did extensive research for Sphere Spirals, searching for a solution to show the open ribbons that form this sphere in a three-dimensional form.

Sphere Spirals is part of a series of prints that demonstrate Escher's fascination for difficult constructions. He saw it as an enormous challenge to visualise complex, three-dimensional objects in such a way that the eye of the viewer understands how they are put together. He often 'opened them up' so that there are glimpses of the inside or the back, parts that would normally be invisible to the eye. Other prints with this property are Two Intersecting Planes, Concentric Rinds, Spirals, Three Intersecting Planes, Rind, Bond of Union, Sphere Surface with Fish, Four Regular Solids and Knots. They are extremely detailed representations of complex and remarkable shapes. But they are also prints that are regarded by many as atypical work for Escher. They are not illusions; the shapes are not impossible. They also appeal to the intellect more than to the heart. Yet these are prints in which Escher's genius clearly manifests itself. He visualised constructs that might exist, but which without his efforts would probably never have come to life. He's showing us something we've never seen before.

Sphere Spirals is not only complex in terms of its shape. Escher needed four blocks of wood that had to fit together exactly to form the end result in four colors. The first wood block, with which he made the proof, also formed the basis in gray for the print Spherical Surface with Fish. In addition, he not only had a hard time with the print itself, he also had a hard time on a personal level. His son George and his wife Corrie had recently emigrated to Canada, and on October 12, 1958, he wrote to them:
'The large flocks of starlings always fly up from the tops of the high beeches, swing around and settle down again in another top. On this quiet Sunday morning, mother and Arthur are not up yet, I keep seeing them swinging by, high above my studio window. They feel the autumn pull within them, they are being called somewhere, their group consciousness is restless.
These days it is very difficult for me to accept my fate when I think about you. That is why I buried myself in sphere spirals.'*
In another letter to George and Corrie he wrote on October 25:
'Ever since you left, I've been chugging my spherical spiral woodcut. After a first proof, my high expectations were - as always - very disappointed. Now, with a little despair in my heart, I am going on steadily, at least to achieve a result that is acceptable.'**
The print was finished shortly after that, but he was not satisfied, something that happened to him quite often. The perfectionist in him kept seeing how it could have been even better.


He confines himself to a sober description of the print ***:
'Here, just as in no. 18 (Sphere Surface with Fish), a sphere is shown with a network of longitudinal and latitudinal circles. Four spirals coil their way around the spherical surface, infinitely small at the poles and broadest at the equator. Half of its yellow exterior is visible. Through open channels in its side the red interior can be followed to the opposite pole.'
If you take a longer look at this print, you will see the sphere start to revolve before your eyes. Just like the revolving red, white and blue spirals barbers used to display outside their shops. Sphere Spirals is above all a testimony to Escher's incredible mastery of his craft and his persistence to bring a complex shape to life.
Although Escher's Sphere Spirals are unique, the concept of 'spirals' is certainly not. In fact, it is a very common form, both in nature and in culture. Think of a snail shell or the shape of galaxies. Peel an apple or an orange and see how the peel is like a spiral circling the spherical fruit. It is also a frequently recurring form in mathematics and architecture. The closest to Escher, however, are the seafarers. When a ship travels across the ocean, the shortest route between A and B is a curved line. The line between the two poles corresponds to the lines on Sphere Spirals. In navigation, this is called a rhumb line (or loxodrome), a curve over the earth's surface along which the course remains the same.




Source
[*] J.W. Vermeulen, Maurits C. Escher, een eigenzinnig talent, Kok Lira, 1995, page 151-152
[**] Wim Hazeu, M.C. Escher, Een biografie, Meulenhoff, 1998, page 404
[***] The 2013 reissue by Taschen GMBH of M.C. Escher. The Graphic Work. Originally published by Royal publishing house J.J. Tijl NV, Zwolle 1959, page 12
More Escher today


A house in the lava
Up early this morning to join the three Germans, the Stern family, on a trip to Giarre by train to see the same lava flow (from 1928) that I already saw and drew three years ago. There, I find a particularly typical subject: a house with a beautiful palm behind it, spared from the heavy lava destruction and completely surrounded by black lava.Escher wrote this in his travel diary on 4 May 1936, detailing his voyage on and around the Mediterranean. The house — the subject of a drawing and (in August) of a lithograph — had (almost) fallen prey to a powerful opponent: Mount Etna.

