Relativity (part I)
The prints of M.C. Escher can be classified in several different ways. For instance, you could group together works that feature never-ending cycles, reflections, or metamorphoses. Or you could categorise them on the basis of birds, reptiles, or stars and planetary tessellations. Escher reckons that his 1953 woodcut, Relativity, forms part of a series in which he stretches the boundaries between the flat image and the three-dimensional plane. In these works, he attempts to combine the different spaces on the flat surface in such a way, that the impossibility of their convergence only becomes apparent on a second or third viewing. He refers to this approach as a study into the:
“relativity of the function of the flat surface.”*
He obviously takes great delight in surprising us with these combinations. With his meticulously worked out compositions, Escher gives us the impression that we are looking at objects, rather than at flat drawings.
The contrast between two- and three-dimensional is however not the main theme of this print. I am more inclined to put Relativity into a series in which he works with rotating motion. If you need to rotate a print to uncover all its possibilities, you are effectively exploring different spaces. In these prints, he almost inconspicuously connects spaces which in reality would not go together.
It is striking how often Escher applies rotating motion in his prints. These rotations are not identical in each print. Anyone who wants to examine Relativity in more detail would do well to hang the print on a rotating frame on the wall. If you were to turn the print clockwise, a different section would appear at the top, but the internal logic would remain intact. The print depicts figures walking up and down a loop of stairs.
This bears a resemblance to the rotating motion in Other world. To truly appreciate the intricacies of this print, we would need to use the same rotating frame as we did for Relativity. Here too, Escher inconspicuously combines different spaces. On the face of it, there is nothing strange about the fact that each window offers a different view. It only becomes strange when you realise which spaces he is combining: across the lunar surface, past the lunar surface and far into the universe. This is only possible if the room happens to be inside a rotating rocket.
In Relativity, a man is pictured walking down a staircase, while less than a meter away another man is walking up the same staircase! See below. How did Escher accomplish this?
How does he manage to deceive us so convincingly? All is revealed when we enlarge details of the print. It’s to do with our perceptions. Escher ingeniously uses the contrast between the foreground and background. As you get closer to the print, you gradually begin to realise where he has tricked us. The bigger the surroundings, the context, the trickier it is to grasp this immediately.
In the image above, the refined quality of Escher’s intervention becomes apparent. The surroundings with the posts, a handrail and a large flower pot have been cut out. Now it becomes clear. The man on the left is obviously walking DOWN the staircase. Look further, and you will see that the man on the right is walking UP the staircase. The man on the left has put his right foot on the white tiles and is about to lift his left foot off the tile. This creates the impression that he is descending. The man on the right is standing with both feet on the darker tiles; he is holding onto the handrail with his right hand, slightly above him. We are looking straight at the white tiles. They are the steps of the staircase, so it appears as though he is ascending. We perceive these two men separately. It is impossible to look at them simultaneously, because the human brain is unable to compute this complex visual perception. We automatically fragmentate what we see; first the man on the left and then the man on the right. That is how Escher toys with our perceptions!
Escher uses the circle in different ways. In 1943, ten years before Relativity, he created his famous work Reptiles, in which he depicts the transition from two- to three-dimensional in a circular motion, a never-ending cycle that is completed and then undone.
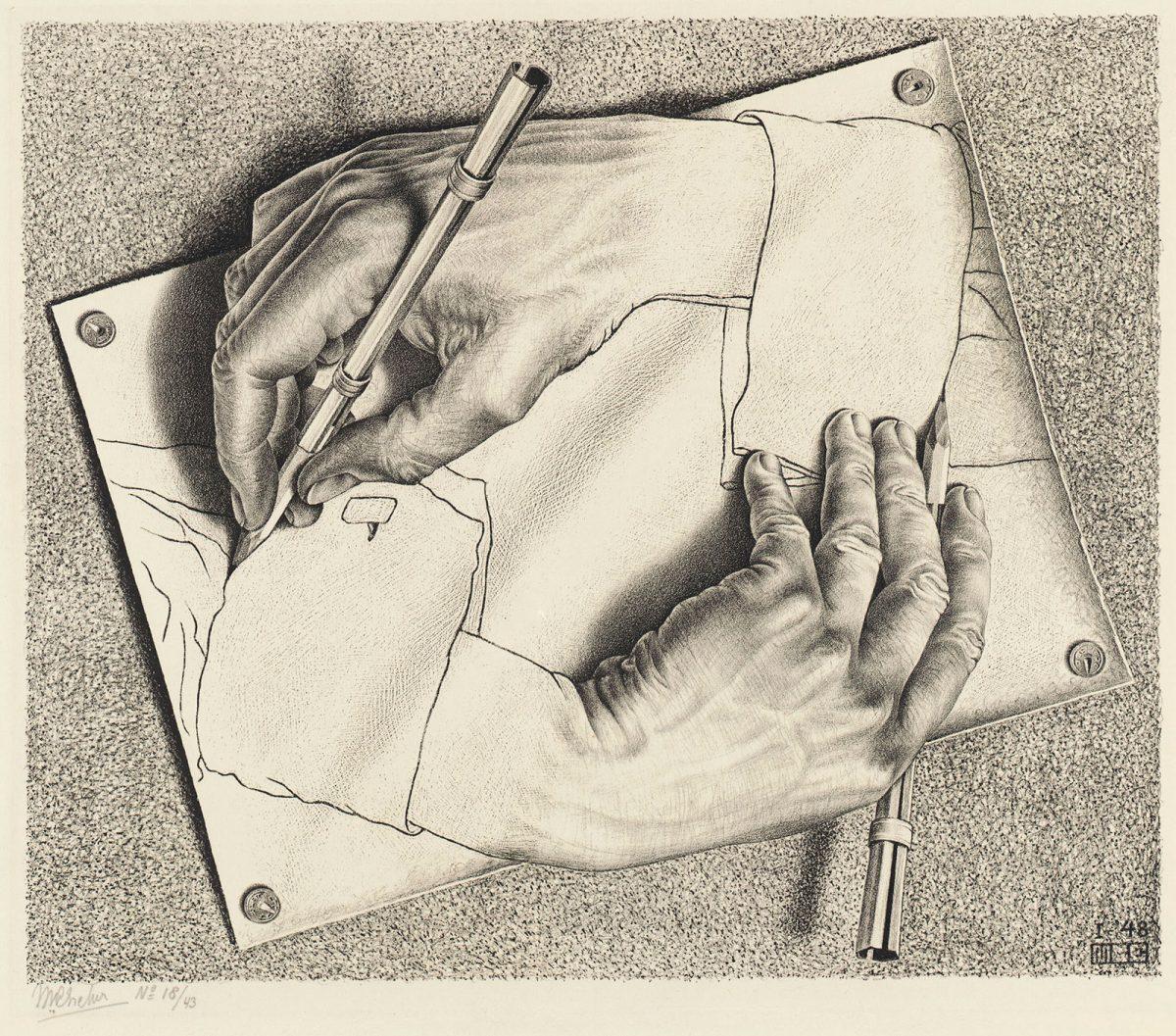
Five years later, Escher creates Drawing hands. In this optical illusion, two hands appear to draw each other, pencilling in the lines of the cuffs. Once again Escher makes us doubt ourselves. What are we actually looking at? The slow transition from two-dimensionality to an optical three-dimensional world is again exceedingly subtle. The image of the hands drawing each other is indelibly etched in your mind. You and Escher keep this circle in motion.
Another five years later, he produces Print gallery, another lithograph. This work is based on a complex mathematical grid that Escher was keen to work out figuratively.
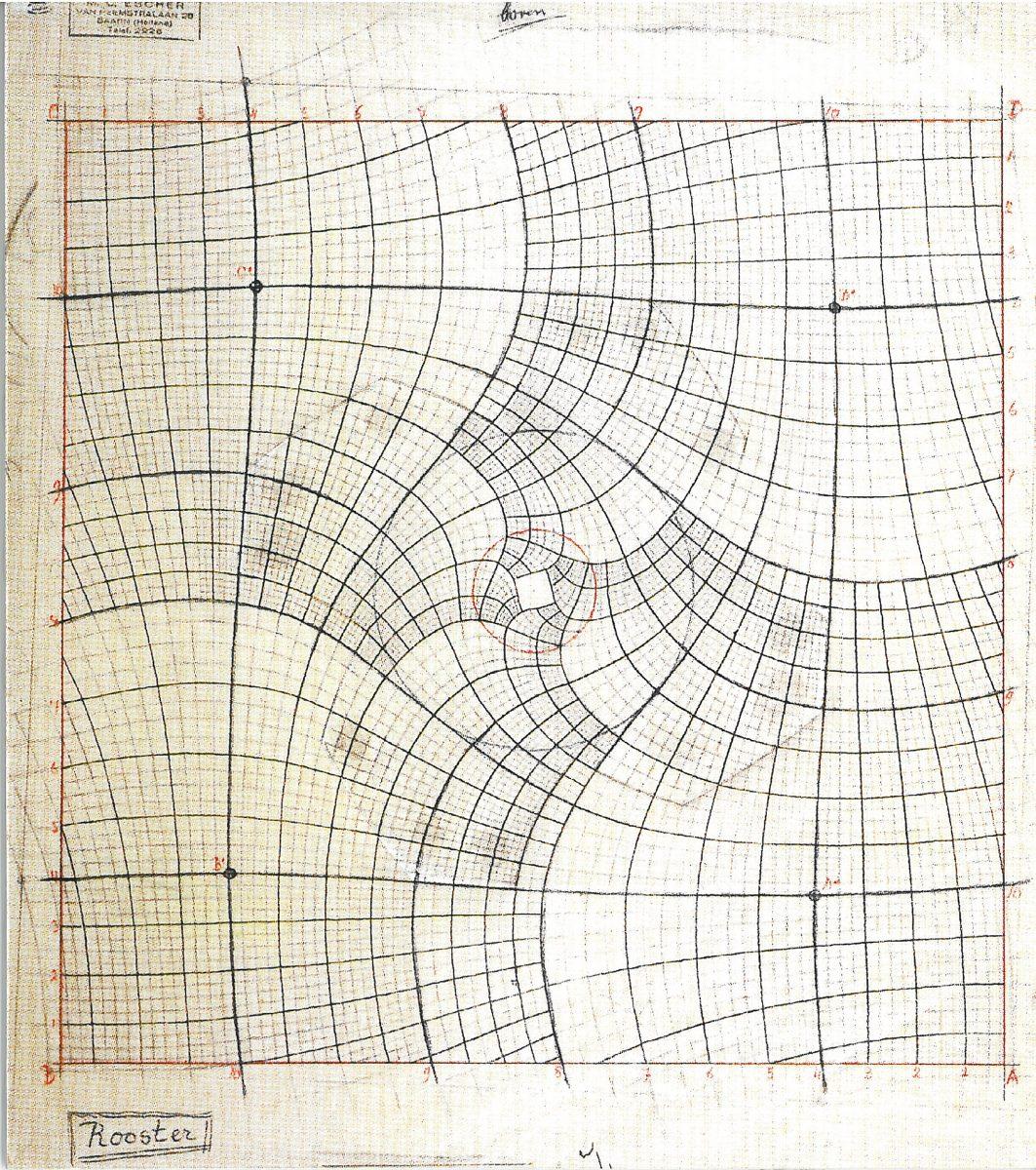
There is a lot going on in Print gallery. Escher describes this in minute detail in the book Grafiek en Tekeningen**:
“We come in through a door in the lower right to an exhibition gallery where there are prints on stands and walls. First of all we pass a visitor with his hands behind his back and then, in the lower left-hand corner, a young man who is already four times as big. Even his head has expanded in relation to his hand. He is looking at the last print in a series on the wall and glancing at its details: the boat, the water, and the houses in the background. Then his eye moves on from the left to the right, to the ever expanding blocks of houses. A woman looks down through her open window onto the sloping roof which covers the exhibition gallery; and this brings us back to where we started our circuit. The boy sees all these things as two-dimensional details of the print he is studying. If his eye explores the surface further, then he sees himself as a part of the print.”
In Print gallery, the interplay between the dimensions is utterly believable because of the circular motion that you make in your head, similar to Drawing hands. Incidentally, Escher used the same mathematical grid in 1959 for one of his most complicated tessellations.
A lot more can be said about Print gallery, for example its setting, but this is best left for another Escher of the Month. It is worth mentioning at this juncture that the Leiden University Mathematical Institute has created an animation that not only explains the mathematical structure behind the grid, but also ‘closes’ the loop itself. The link is shown at the very bottom of this article.***
Fish and Scales has an almost abstract quality because of the intricately interwoven patterns that are unmistakably fish-shaped, but can also be seen as geometric shapes. You need to view this work from a distance and unfocus your eyes slightly so that the details disappear. Otherwise, you will mostly see a magical aquarium onto which a magnifying lens has been stuck.
Although the lithograph Up and Down (1947) is not about rotation, an infinite circular movement can indeed be detected. You, the viewer, are positioned in the centre of the endlessly repeating strip. Now imagine this strip continuing until the loop closes and picture yourself as the axis of this wheel as the strip rotates around you from top to bottom.
After Metamorphosis II (1939-40), infinite circular motion features regularly in the prints of M.C. Escher.
Sources of quotations:
* p. 73: relativity of the function of a flat” in Escher on Escher – Exploring the infinite; with a contribution by J.W. Vermeulen; translated from Dutch by Karin Ford; Abrams, New York 1989
** 2006 Reprint, published by Taschen GMBH of “M.C. Escher Grafiek en Tekeningen”; ingeleid en toegelicht door de graficus; originally published by Koninklijke uitgeverij J.J. Tijl NV, Zwolle 1959.