The Roger Penrose puzzle

In May 1971, Escher produced his final tessellation, a drawing in India ink and watercolour of a figure that he himself called a ‘little ghost’. It was the last in a long series of tessellations produced in notebooks, but it was also a remarkable drawing in another respect.

In 1962 the British mathematician Roger Penrose travelled to the Netherlands and he visited Escher in his house in Baarn. The two had got to know each other after Penrose saw work by Escher during the International Mathematical Congress in 1954. They started an exchange of letters that would lead to the print Ascending and Descending in 1960. Throughout his career Penrose was fascinated by tessellations, a fascination that he shared with Escher. Penrose received a print from Escher and in return he gave his host a wooden puzzle. It consisted of a series of identical geometric shapes based on a rhombus. Two sides of the rhombus had been modified by cutting out a trapezoidal shape with angles of 60 and 120 degrees and positioning it on the other sides. The shapes fitted together in many ways, but there was only one unique way in which they could be combined to create a tessellation containing all the puzzle pieces. The mathematician challenged the graphic artist to solve the puzzle. Escher accepted the challenge and puzzled over it for a while, until a few weeks later he was able to send Penrose a letter outlining the solution. In the letter, Escher expressed his astonishment that the forms only fitted together in one way. It went against the belief he had held for many years that a tessellation, by means of various reflections and rotations, could be continued indefinitely.

The Art of the Impossible: M.C. Escher and Me

In this two-part documentary Roger Penrose talks about his relationship to Escher. His puzzle is also mentioned. See also Escher on film.

But solving the puzzle was not all. Penrose’s basic shape prompted him to create his own version. In a letter to Penrose, he drew the figure he had devised and described it as his ‘little ghost’. After that, it was several years before he produced a tessellation with this shape in May 1971. It was a unique tessellation for two different reasons. It is the only one in his oeuvre of hundreds of drawings and prints that cannot be repeated randomly. And it is also the last drawing that Escher is known to have produced.

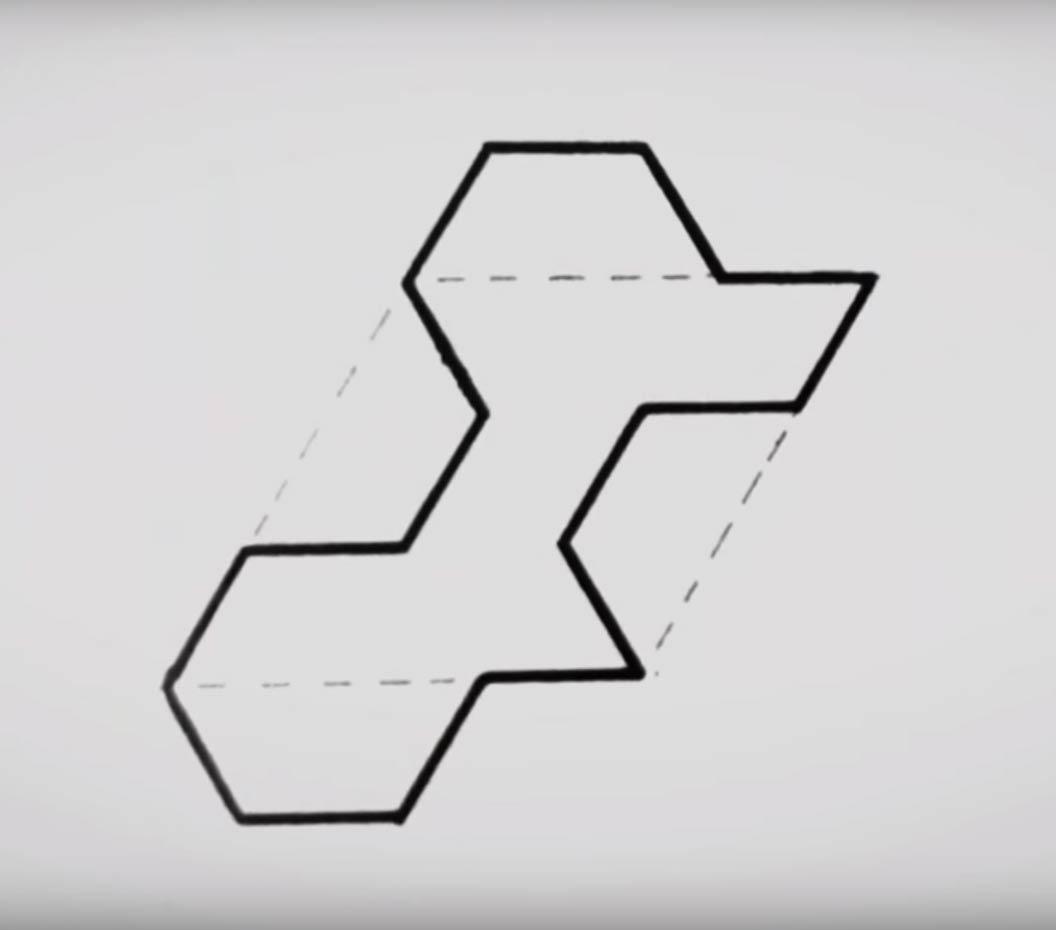
The search for a non-repeating tessellation

Penrose kept himself busy too. He continued trying to devise a tessellation that would never repeat itself horizontally or vertically. For a long time it seemed impossible that such an infinite surface could be filled in an ordered pattern without becoming repetitive. That is what all mathematicians believed until the 1950s. A tessellation of repetitive forms must be able to extend to infinity. If the basic tiling can be continuously repeated, then it is periodic. However, a consensus gradually formed around the notion that it must be possible to create a tessellation that could not be repeated randomly. Roger Penrose wrote an article about it for the Christmas edition of New Scientist in 1958, together with his father Lionel Penrose. In it, they encouraged readers to puzzle over these aperiodic tilings, based on seven different basic forms.

In 1974 Penrose invented an aperiodic tiling which consists of only two basic shapes. The shapes he came up with were a dart and a kite. Pushed together in the most obvious way, they form a rhombus. But that is precisely the way in which they cannot be combined if you want to create an aperiodic tiling. The red and green lines in the sample forms below indicate how they can be combined; the lines must merge. Later it turned out these aperiodic tilings could be created from a second pair of shapes: a sharp and a blunt rhombus with angles of 36 and 144 (sharp) and 72 and 108 (blunt) degrees, i.e. all multiplications of 36. The ratio of darts to kites and of sharp to blunt rhombi is always the same in a Penrose tiling. Namely that of the golden ratio, 1: 1.618. In other words, if a Penrose tiling contains 100 darts, it will contain 162 kites. The greater the numbers, the closer the ratio is to that of the golden ratio.

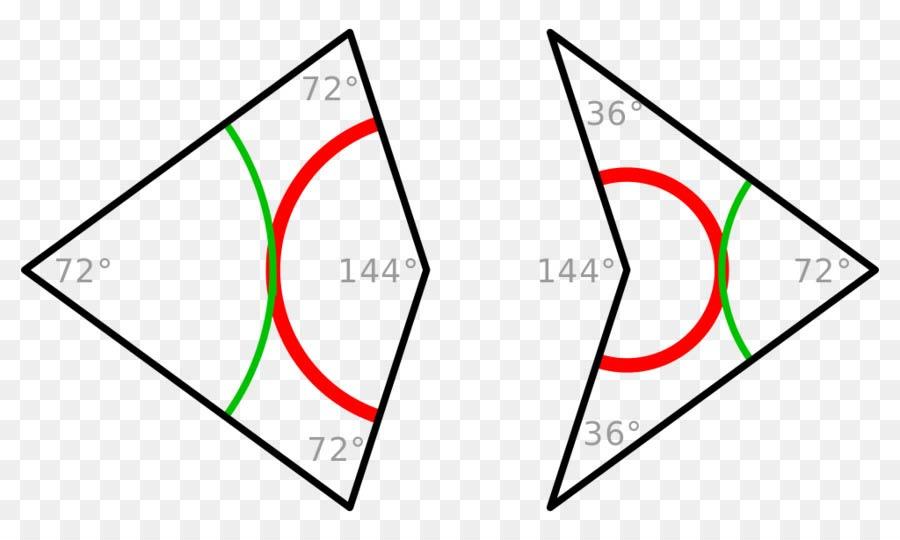
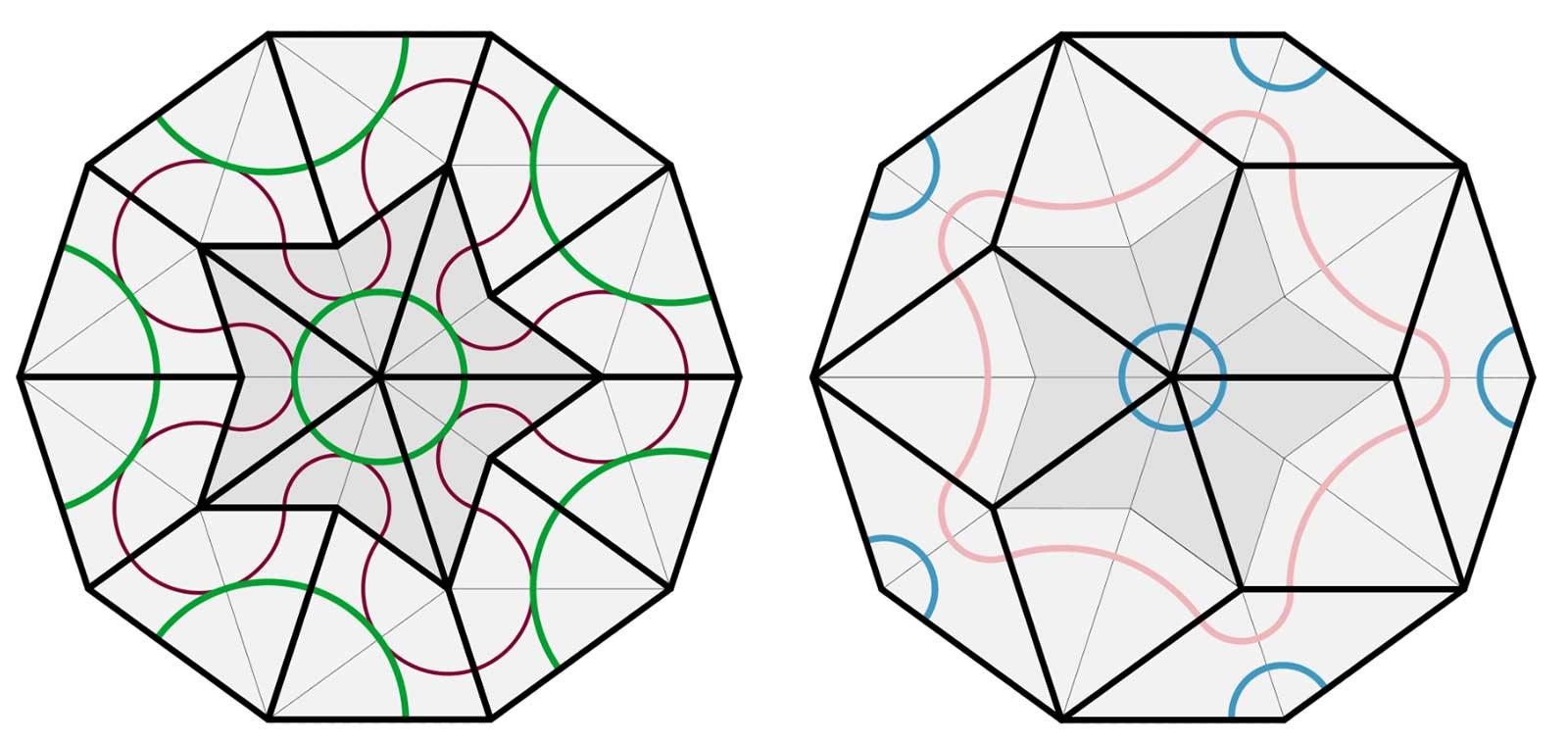
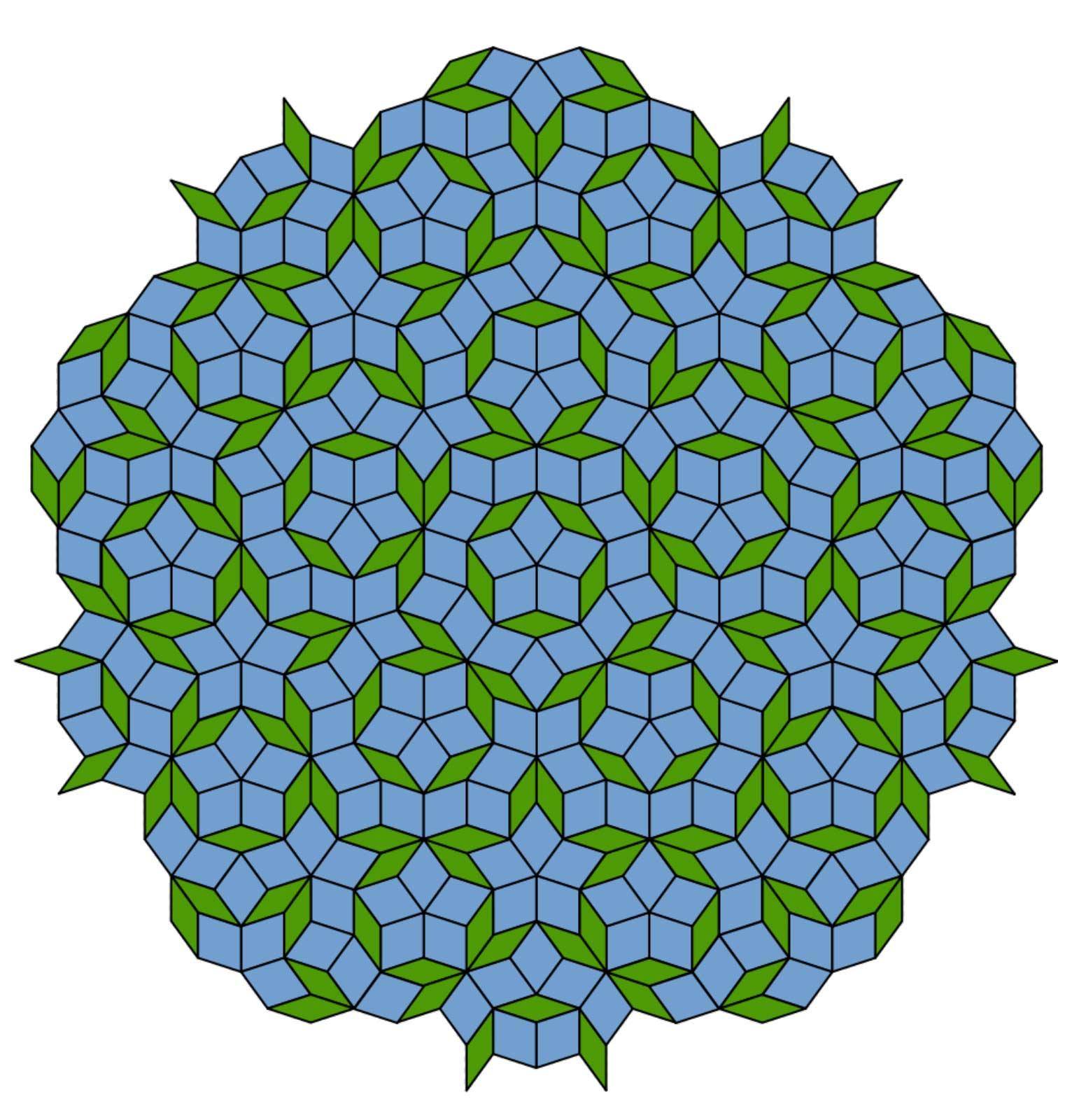
In his article Pentaplexity, published in the mathematical journal Eureka in 1979, Penrose described his search for aperiodic tilings.

Scientific journalist Martin Gardner devoted two of his Scientific American columns to aperiodic tilings. In 1988 the columns, including those about Penrose, were included in the book Penrose Tiles to Trapdoor Ciphers.

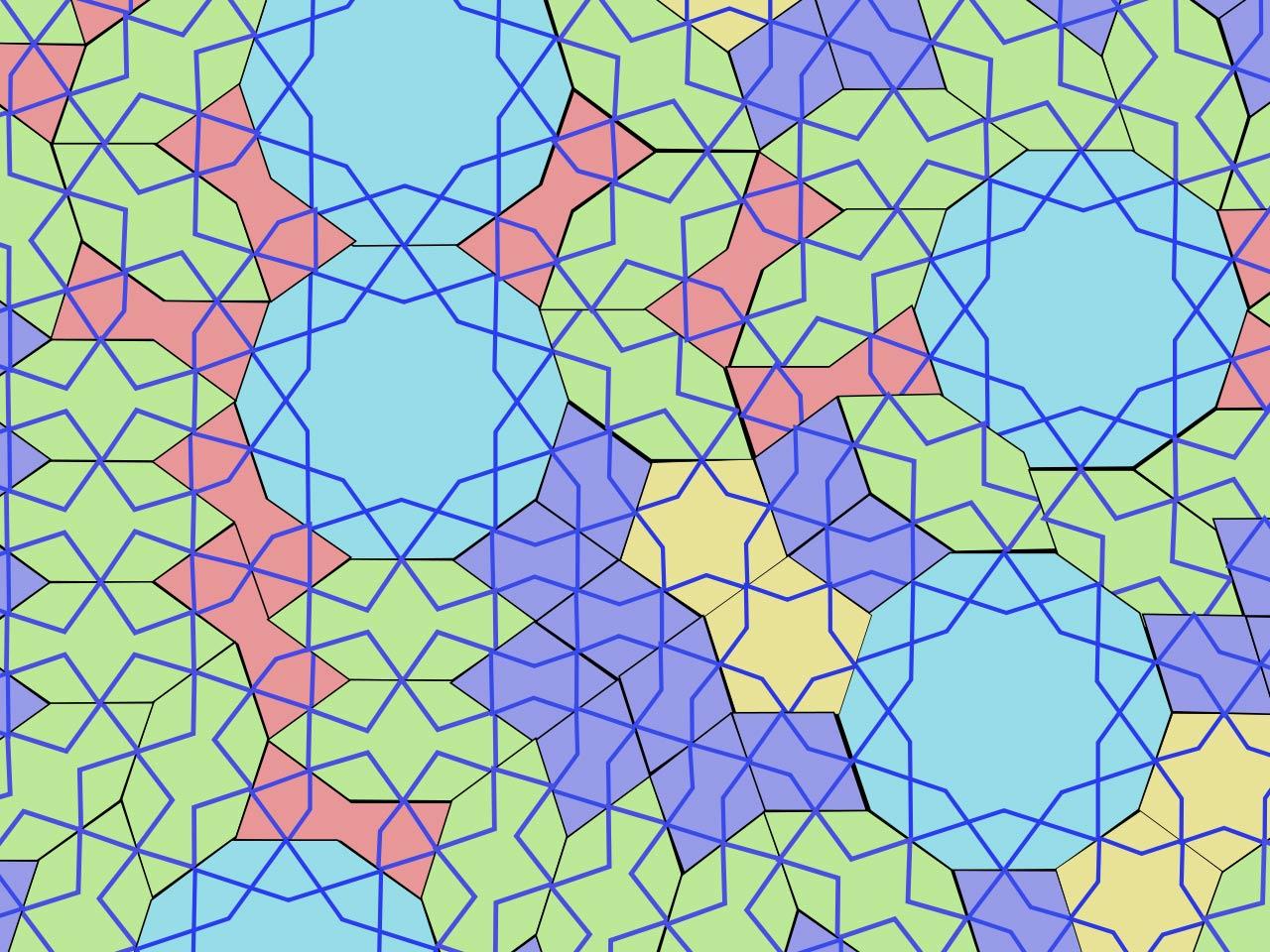
In the February 2007 edition of Science, Peter Lu and Paul Steinhardt published their research into patterns in early medieval Islamic art. They discovered that they already contained tessellations with non-repeating patterns. One such example is the arch of the 15th-century Darb-i Imam burial complex in Isfahan, Iran. It is decorated with a tile mosaic that is ordered but contains no repetitions. Although there is debate among scientists when exactly those patterns were applied, it is certain that they were only discovered in the West hundreds of years later.

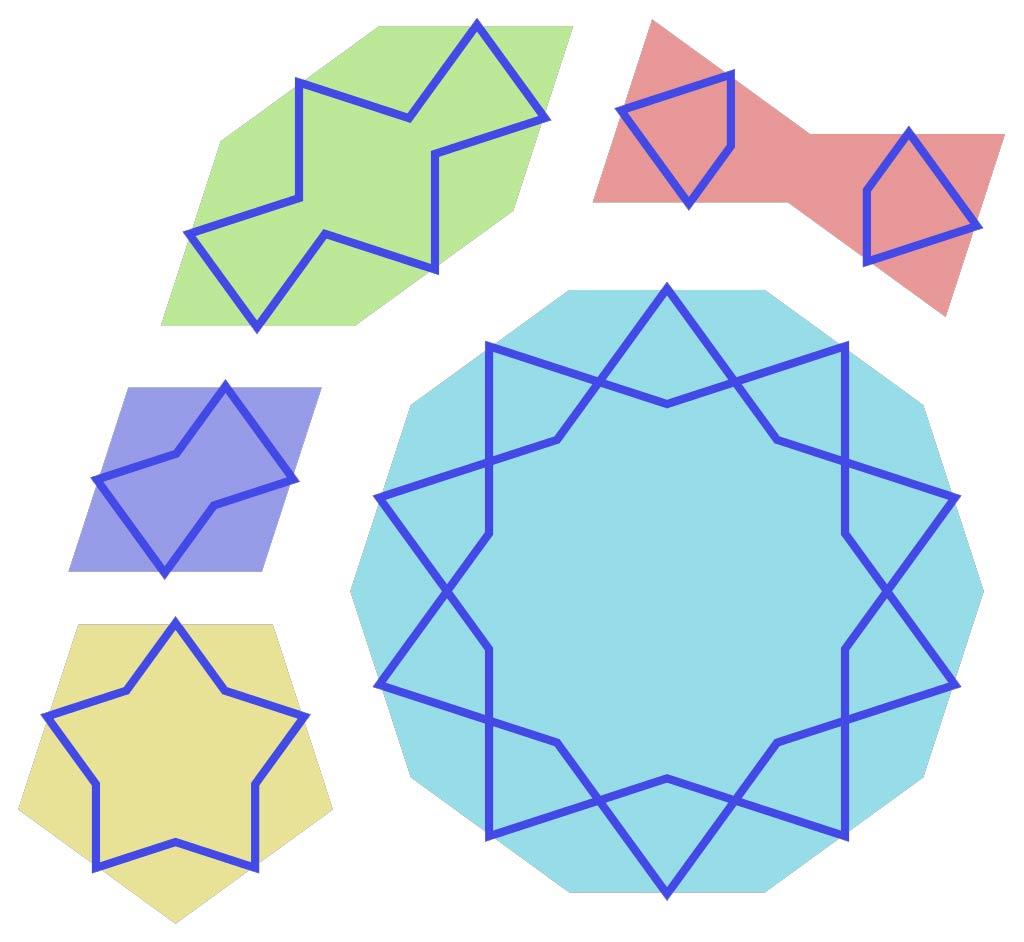
Girih tiles

Researchers Lu and Steinhardt discovered five different tiles in the Islamic patterns. These ‘Girih tiles’ (Girih literally means ‘knot’) were probably in the toolbox of every craftsman who was working on the buildings at the time. A rhombus, a bow, a regular decagon, a regular pentagon and an irregular hexagon. The Girih tiles allow both periodic and aperiodic tessellations to be created. All sides of these five tiles are exactly the same length. Tiles of the same shape can be added, all of which are reduced by the same factor. Thus making the most wonderful configurations possible.

Our exhibition Nadir and Zenith in the World of Escher featured Penrose tilings too. During the research process for his print book, illustrator Wouter van Reek came across them and even produced some himself. They were very subtly incorporated into the eponymous print book, which was released on 23 May 2019.

These two beautiful animations by Maurizio Paolini and Alessandro Musesti from the university in Brescia provide a clear account of how a Penrose tiling works.