Horseman

Broadly speaking, admirers of the work of M.C. Escher can be divided into three groups. The first and most obvious group comprises those who enjoy optical illusions. The second group consists of mathematicians, or people who in one way or another deal with mathematics in their daily lives. They regard Escher as the undisputed master of tessellated art, who used the abstract concept of “the 17 plane symmetry groups” to maximum effect to create illustrations that they could deploy in their profession. The third and final category of Escher admirers consists of the casual observers who simply enjoy looking at his prints. They are not specifically looking for an optical illustration, nor are they interested in tessellation as a standalone theme. They derive aesthetic pleasure from his prints, and are frequently dazzled by Escher’s imaginative mind.

I cherish all of our visitors, but this third group is perhaps my favourite, because I never tire of seeing that look of amazement on their faces when they come face-to-face with Escher’s work. They will always find something that amazes them, or makes them happy. Although I devised a thematic layout for Escher: Eternity & Infinity, the exhibition follows a more or less chronological course. That is to say that, slowly but surely, and little by little, the themes develop over time. Occasionally Escher shifts his artistic attentions elsewhere, only to revisit the subject matter years later.

The tessellation is a striking example of this. As far back as 1920 or 1921, while still a student, Escher created two works of art that bear a striking resemblance with a tessellation:

The two feature the same pattern of a sitting and a lying Buddha-like male figure. These patterns have been interlocked and framed in different ways to create the illusion that they are different. In addition, he applied a different technique in the second work of art: on the left is a lithograph and on the right is a woodcut. To accentuate the difference even further, Escher applied colour in the lithograph.

In 1922, he follows up these two prints with Eight Heads.

In 1922, he visits Spain and Italy. In the Alhambra, the Spanish-Islamic citadel and palace in the Spanish city of Granada, he copies a single mosaic wall tile, only one of the many decorative mosaics that adorn the building. Fourteen years later, things are very different.

He spends the next thirteen years living and working in Italy, and – with a few exceptions – devotes little attention to tessellations. This is probably also the reason why most people mistakenly believe that his interest in tessellations only began in 1935, the year that the Escher family leaves Italy. In 1936, Escher and his wife Jetta journey by boat along the coasts of Italy and France to Spain. They travel the length and breadth of Spain and make a return visit to the palace of Alhambra in Granada and the Mezquita, the great former mosque of Córdoba. In both places, they copy sections of the mosaics found on walls and ceilings and the upper sections of the Mezquita in Córdoba. A year later, Escher incorporates the first tessellation as a narrative element in the woodcut Metamorphosis I.

Here, he depicts the transition of the small Italian town of Atrani via geometrically rigid patterns of cubes to a freestanding figure. Later that same year, he shows this print and some of his sketchbook drawings to his half-brother B.G. (Beer) Escher, a professor of geology at the University of Leiden and a specialist in crystallography. Beer reacts enthusiastically to what he sees. Suspecting that Escher might be interested in the latest developments in crystallography, Beer sends his younger brother a short bibliography, including an article written by the Hungarian scientist George Pólya defining the 17 plane symmetry groups. (*)

The article’s closing sentence is to make a lasting impression on Escher:

“Elsewhere in this paper, I shall explain why I believe that my mathematical study of these ornaments may also be of artistic interest.”

According to Dr. Doris Schattschneider, an expert on Escher’s tessellations, Escher’s discovery of Pólya’s 17 plane symmetry groups, along with the definition of “the regular division of the plane” in a paper written by the Professor F. Haag in 1923, constitute the evolutionary breakthrough in the tessellated art of M.C. Escher. (**)

In an article penned in 1947 for Phoenix, Monthly Journal of the Visual Arts, as well as in subsequent writings, Escher almost verbatim copies Haag’s definition when describing his tessellations:

“A plane, which one must imagine as extending without boundaries in all directions can be filled or divided into infinity, according to a limited number of systems, with various and increasingly complex geometric figures that are contiguous on all sides without leaving empty spaces . When one seeks to fit such congruent figures together in such a manner, that they arouse within the viewer associations with something familiar, such as an object or a living creature, then a fascinating game emerges, because it affords the artist infinite possibilities yet also confines him to the limitations imposed by the rules of play.” (***)

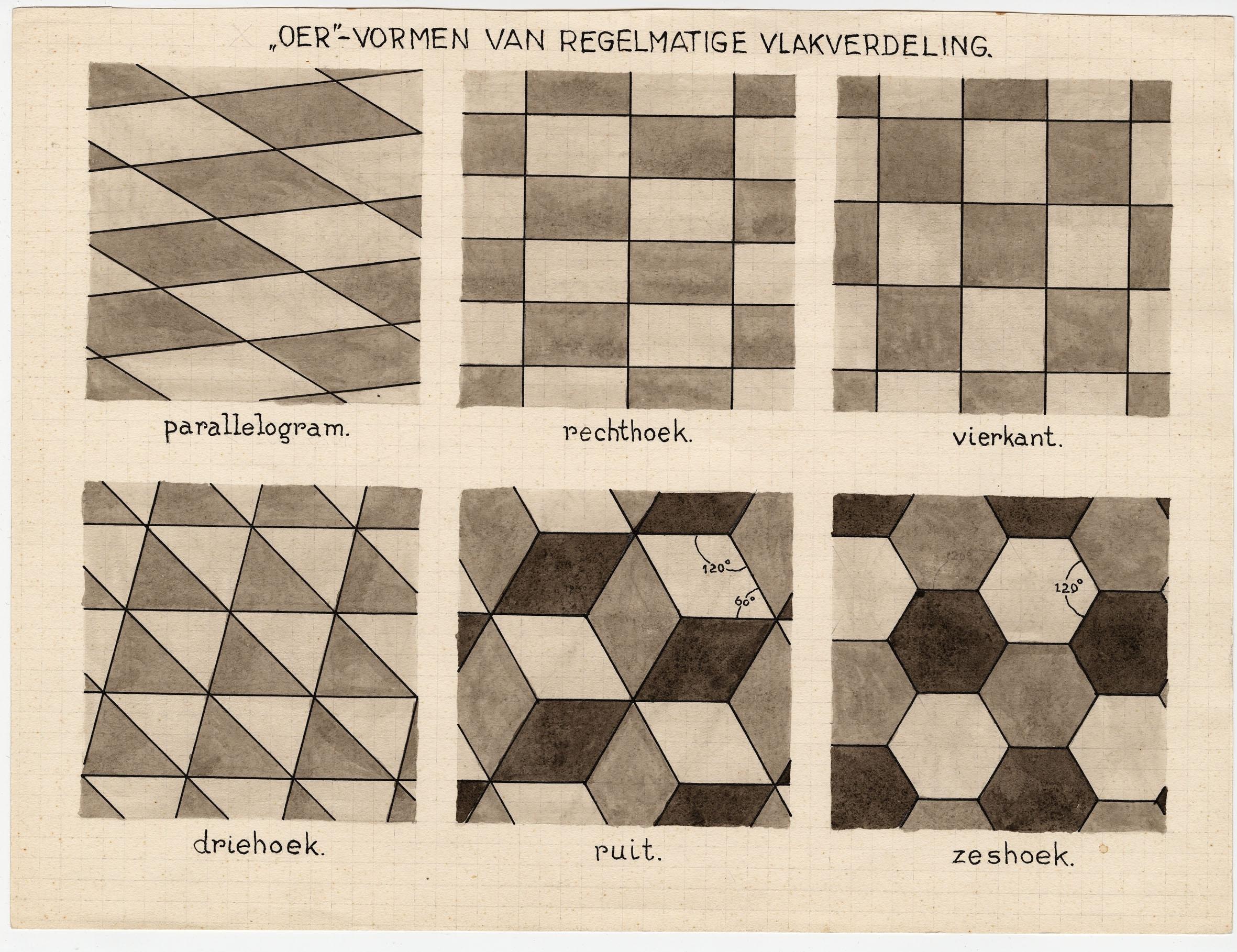
During the war years, Escher spends most of his time working out Pólya’s 17 plane symmetry groups. Whereas Pólya focusses mainly on the abstract, straight patterns of the Arabic tiles, Escher slowly but surely transforms these series into curved, “swinging” designs. In the 1960s, in preparation for a series of lectures that he was about to deliver, he drew a set of simple examples. These examples seem so simple that one can almost be forgiven for believing that even laymen – such as myself – are capable of creating a similar variation with just a little preparation. But I know only too well that I will never succeed, not in a million years! Escher starts off with easy tessellations, looking like pavement and bathroom tiles, before moving on to the hexagonal shape of a honeycomb:

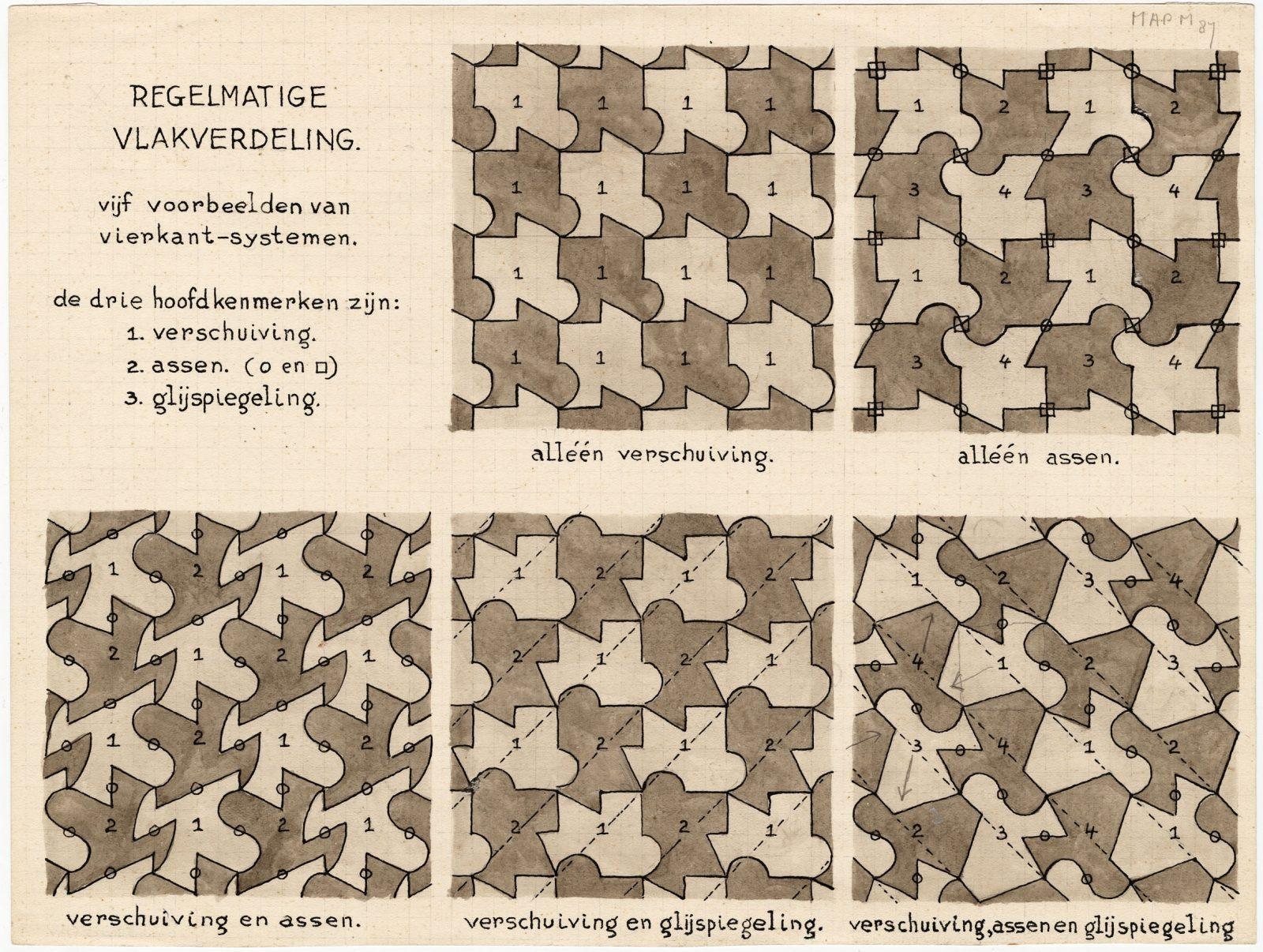
Things soon become more complicated, however. Whilst the first two planes of the next examples are relatively easy to comprehend, the last three are completely incomprehensible to non-mathematicians like myself:

The wonder of Escher, of course, lies in his ability to turn these abstract figures into artistic representations of birds, fish, reptiles, dogs and horsemen!

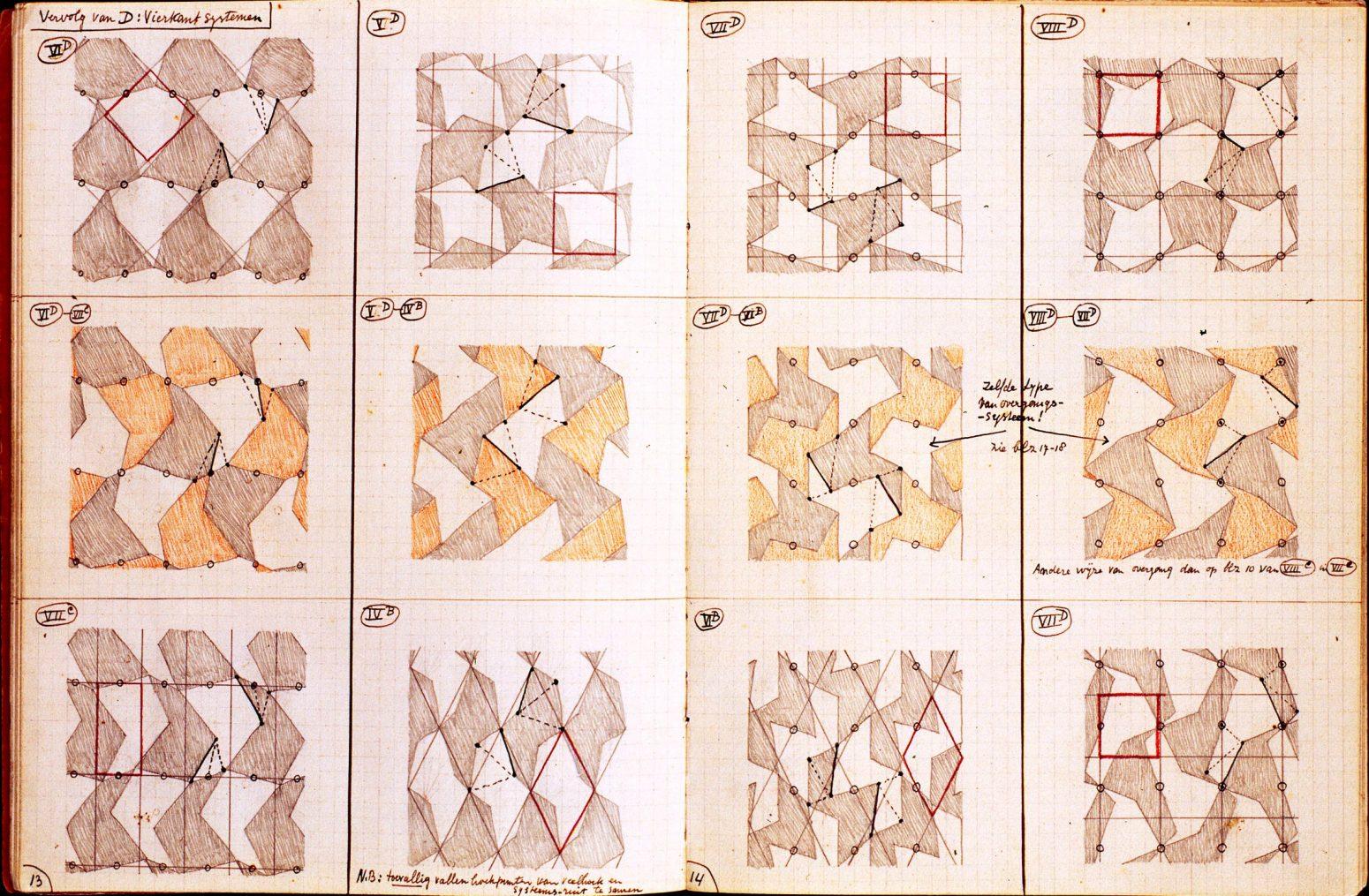
Having tirelessly worked out the 17 different geometric diagrams of George Pólya and unlocked their infinite possibilities, Escher begins to adopt a more playful approach to his work.  His remarkable ability to ‘think out of the box’ enabled him to tranform abstract concepts into recognizable figures. Below is a page from one of his notebooks.

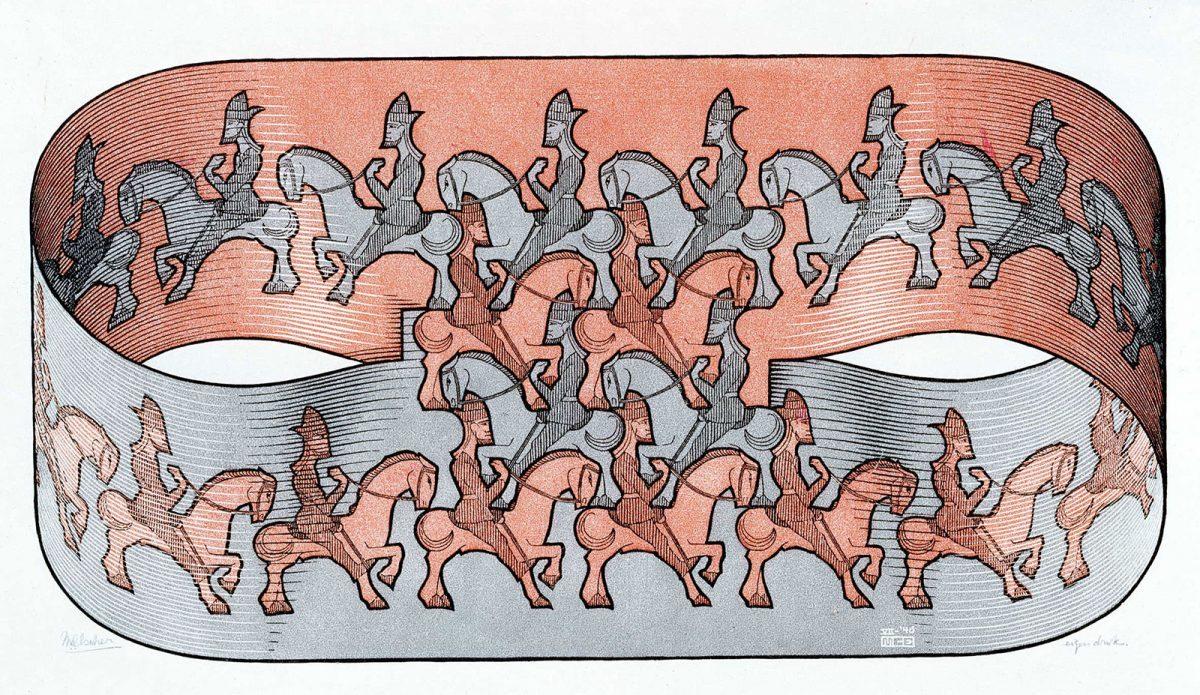
Horseman, like so many of Escher’s other works, isn’t ‘just’ a tessellation. He combines the tessellating pattern of the horseman with a so-called Möbius Strip, the figure of eight.

The parade of red and grey horsemen – with the grey horsemen moving to the left and the red horsemen travelling to the right – form a tessellation in the centre of the piece. The grey horseman is depicted against a red background and the red horseman is depicted against a grey background. Or, as Escher puts it in his Phoenix article:

“as if it were a woven fabric: the “pattern” in the foreground has the same colour as the “background” on the reverse side, and vice versa. The two form a closed circle.”(****)

Horseman is only one of many prints in which tessellation features prominently. Escher combines tessellation with optical illusions, as well as with representations that only exist in our heads. His works never cease to amaze, surprise and delight us.

Footnotes:

*) G. Pólya: Über die Analogie der Kristallsymmetrie in der Ebene; Zeitschrift für Kristallographie, 1924
**) D. Schattschneider Visions of Symmetry, pages 21 to 29 incl.
***) Phoenix, monthly journal of the visual arts, Volume 2, No. 4, June 1947; in the column ‘Graphic Artists of the Netherlands Speak of Their Work’.
****) Idem III