Development I

Development I and Development II are both prints in which Escher attempts to find a satisfactory way to express the concept of ‘infinity’. They show development, but are also part of a development. In October 1937, he showed his collection of tessellations to his brother Beer (Berend), a professor of geology, mineralogy, palaeontology and crystallography at Leiden University. Escher’s collection consisted partly of copies of tessellations he had traced in the Alhambra (Granada) and La Mezquita (Cordoba) in the spring of 1936 and partly of ones he had drawn himself. He first started making tessellations some ten years earlier. In his early attempts, he carved an animal shape directly into the woodblock, after which he duplicated it on paper or fabric either mirrored or rotated.

‘I needed at least three colours to cover my stamp block in order to get one pattern to contrast with the repeating congruent repetitions of that pattern. I exhibited these stamped works, but had little success with them. It was partly due to circumstances that it wasn’t until 1936 after a second visit to the Alhambra that I devoted a large part of my time to toying with animal shapes. What interested me most was the dual function of the dividing line between two adjacent figures, as it is equally as indispensable for one pattern as for the other. The ‘discovery’ of such a pattern which, according to a certain system, repeats itself rhythmically and as such is dependent on unwavering laws, has always been and continues to bring me great joy. It offers the sensation of approaching something both ancient and eternal. *’

Although he very much enjoyed making these tessellations, he had little success selling them. This was partly why it took until his voyage in 1936 to the Alhambra before he recommitted fully to this art form. He came to the conclusion that using a wooden block to print a tessellation was far too tedious and that it would take a long time for him to make any progress. He had to study the tessellation concept much more systematically, so he began drawing them in notebooks with squared paper. The grid on the pages helped him visualise the patterns. Beer was impressed, partly because he realised that his brother lacked the scientific background with which he himself had examined the patterns. He explained that his brother actually created a kind of “crystallography on a flat surface”. He advised Maurits to read the Zeitschrift für Krystallographie und Mineralogie (established in 1877). Maurits managed to read through a number of volumes in Brussels.

This trade journal turned out to be too difficult and theoretical to truly interest him, but there was an article that intrigued him: Über die Analogie der Kristallymmetry in der Ebene (1924) by the Hungarian professor George Pólya **, who lived in Zurich. In it Pólya defined 17 different geometric systems with which a tessellation could be made. For Escher, it was not so much the underlying theories that he was interested in, but its visual interpretation. Pólya had made a drawing of each system. Escher was fascinated by that visual proof and copied the 17 systems in his notebooks. In the final paragraph of his article, Pólya mentioned that his systematic layout of tessellations was not only interesting for mathematicians, but could also be of interest to artists.

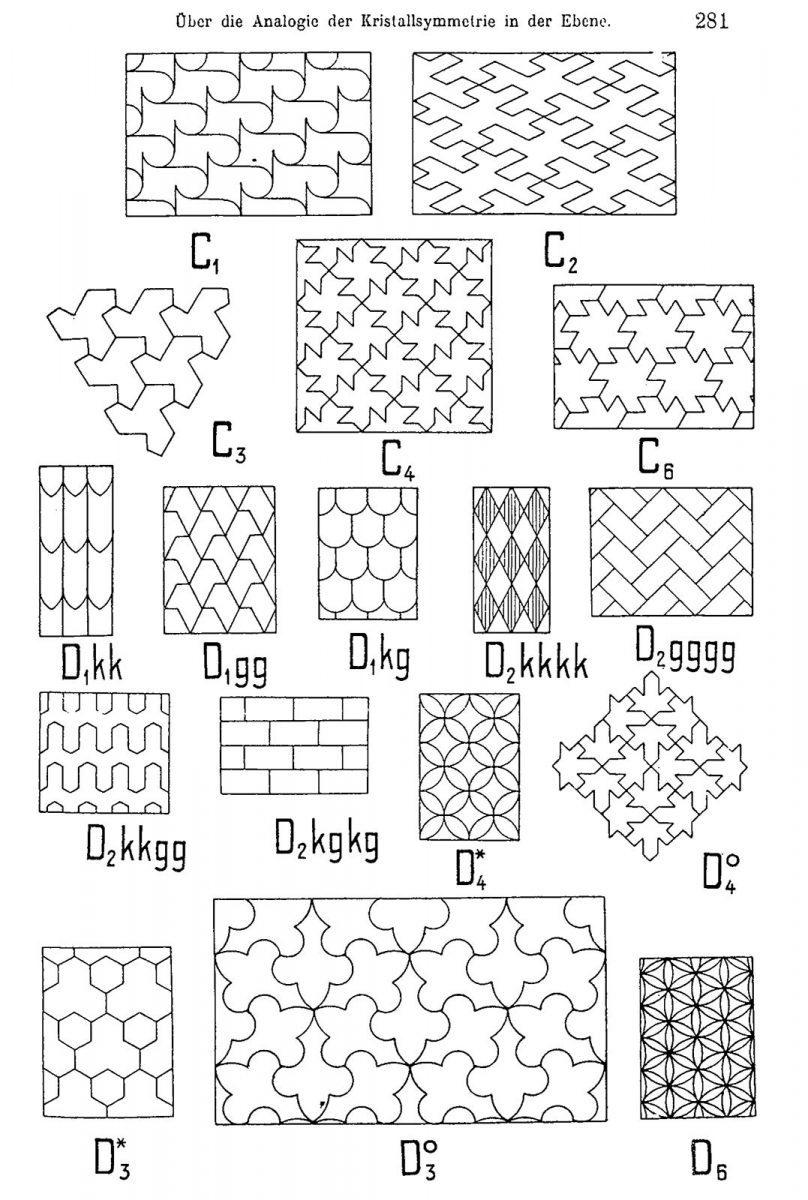
During that same time period, Beer also steered him towards the work of the German crystallographer Friedrich Haag ***. In his article Die regelmässigen Planteilungen und Punktsysteme (1923), he also describes a series of systems with which a tessellation can be made. In it, Escher also finds a definition of one for the first time:

Die regelmäßigen Planteilungen bestehen aus kongruenten, lückenlos aneinandergereihten konvexen Polygonen; die Anordnung der Polygone um jedes einzelne ist die nämliche wie ein jedes andere.

The definition may be a bit dry, but it does strike a chord. Someone has formulated a phenomenon in writing that was gradually starting to fascinate him. He also copied Haag’s definition in his notebook. In the autumn of 1937, he began sketching and fanatically practicing the systems of both Pólya and Haag and made considerable progress in his understanding of tessellations. For Escher, the discovery of these scientists truly was a Eureka moment. He was not alone in his fascination; in fact, there was a scientific foundation for it. The patterns in the Alhambra and the articles by Pólya and Haag thus formed the basis of his lifelong search.

Whereas Pólya and Haag mainly relied on abstract Arabic tile patterns, Escher succeeded in bringing these series to life by giving them animal forms. The first result in print form was the woodcut Development I from November 1937. He used a tessellation of reptiles that he based on the Pólya system. The tessellations he made prior to this were still quite static. Based on his own research into tessellations, he did not progress beyond a grid of squares, diamonds and parallelograms from which the animals have difficulty escaping. The Pólya and Haag systems gave him a direction for further experimentation, although squares also form the basis here. He made two drawings, of which only the first is found in our collection. Both are drawings in which he uses reptiles for the first time. In the first drawing, they are circling each other in four directions with their mouths closed. In the second drawing, the pattern is open, giving the drawing even greater dynamics.

In the print itself, he also applies a very compelling pattern of squares. It is a chessboard that, as the gaze moves towards the centre, transforms into the four central reptiles. Given his fascination for the game of chess, this pattern was obvious, but also necessary as a foundation for the transformation. In a letter to friend Hein ‘s-Gravezande ****, he describes the print as follows:

‘…the purest, that is to say the one that, without any concessions, inhabits an idea in the best and most logical sense; it became therefore also the driest and least ethical. The ‘development’ takes place gradually in two ways: in tone contrast and in form, which means that, at first (on the edge), everything is grey and then develops into pure black and white in the centre while, as far as the shape is concerned, the square develops gradually from the edge towards the centre, transforming into a complex animal contour.’

Escher also created a chessboard that transforms into a tessellation of reptiles in Metamorphosis II, which he drew in the winter of 1939-1940. He has the reptiles from Development I transform into those from Development II. At that point in his life, he was very enthusiastic about these prints and the direction that his career was taking. Later on, he also understood the limitations of the manner in which he showed the transformation. For example, in 1956 he says about Development I in his own book M.C. Escher – The Graphic Work:

‘Scarcely visible gray squares atthe edges evolve in form and contrast towards the centre. Their growth is completed in the middle. An unsatisfactory feature of this kind of  inward-directed unfolding is that there is so little space left for the freedom of movement of the most greatly developed figures: two white and two black reptiles.’

For Development II, he reversed the direction. The metamorphosis starts at the centre and grows as it gets closer to the edge, ending in adult reptiles. But, in the end, this print did not satisfy him either, as the edge of the paper now determined the end of the transformation. He continued to look for the best form in the years that followed, but kept encountering the limits of paper. This is clear in such prints as Division, Smaller and Smaller, Regular Division of the Plane VI, Path of Life I and Path of Life II. Only when he discovered the circle limits did he find the perfect shape: a circular tessellation that becomes increasingly smaller towards the edge and can therefore continue indefinitely -like a planet filled with tessellations.

Source:
[*] M.C. Escher: Hoe ik er toe kwam, als graficus, ontwerpen voor wandversiering te maken. In De Delver, 14th volume, March 1941. This art journal, published between 1927 and 1941 by ‘Stichting De Delver’, wrote intensively about graphic art. Escher published multiple times in it.

[**] G. Pólya: Über die Analogie der Kristallsymmetrie in der Ebene; Zeitschrift für Kristallographie, 1924

[***] F. Haag: Die regelmässigen Planteilungen. Zeitschrift fur Kristallographie 49 (1911) page 360-369 and F. Haag: Die regelmässigen Planteilungen und Punktsysteme. Zeitschrift fur Kristallographie 58 (1923) page 478-488

[****] Wim Hazeu, M.C. Escher, Een biografie, Meulenhoff, 1998, page 248