Circle Limit IV (Heaven and Hell)
In July 1960 Escher completed the last of his four ‘circle limits’. He had struggled with it for a while, but it was a publication by the Canadian professor H.S.M. Coxeter that set him on the right path. He had met this professor at the University of Toronto in 1954, during the International Congress of Mathematicians. In the article, Coxeter described how a tessellation from the centre to the edge of a circle is increasingly reduced and the motifs come to lie infinitely close together. In 1957 Coxeter gave a lecture for the Royal Society of Canada and he asked Escher by letter if he could use a few of the graphic artist’s works in the lecture. Afterwards, Coxeter sent Escher a copy of his lecture (which had been published under the name Crystal Symmetry and its Generalizations), in which he also included the figure about which Escher would become so enthusiastic. Coxeter in turn based this figure on the work of the French mathematician Jules Henri Poincaré, who visualised this form of hyperbolic geometry in his Poincaré disk.
Escher primarily drew inspiration from the illustrations, not being able to do much with the accompanying text:
‘Coxeter’s hocus-pocus text does nothing for me, but the picture will probably help me to create a tessellation, which promises to be a completely new variant of my series of tilings of the plane. A circular, regular tiling, which is logically bounded on all sides by the infinitely small, is something wondrous. Almost as beautiful as the regular tiling of the sphere. At the same time I have the feeling I am getting increasingly further removed from what I can achieve “success” with the “public” with. But what can I do about it, if a problem like this fascinates me so much that I cannot shake it off? It is less easy than it seems. Try it: put one (or four) squares of any size in the middle of a circle (e.g. separated by two perpendicular diameters) and gradually reduce them to the outside, and so on, such that they line up like chessboard squares. You will not get there with only fourfold axles; you have to alternate the four-tier with six-tier in a most curious manner, which is normally impossible on the flat surface. The boundaries are therefore only rectilinear to a limited extent (only three intersecting middle lines) and aside from that they are all circles. Without Coxeter’s image I would never have come up with the idea.’*
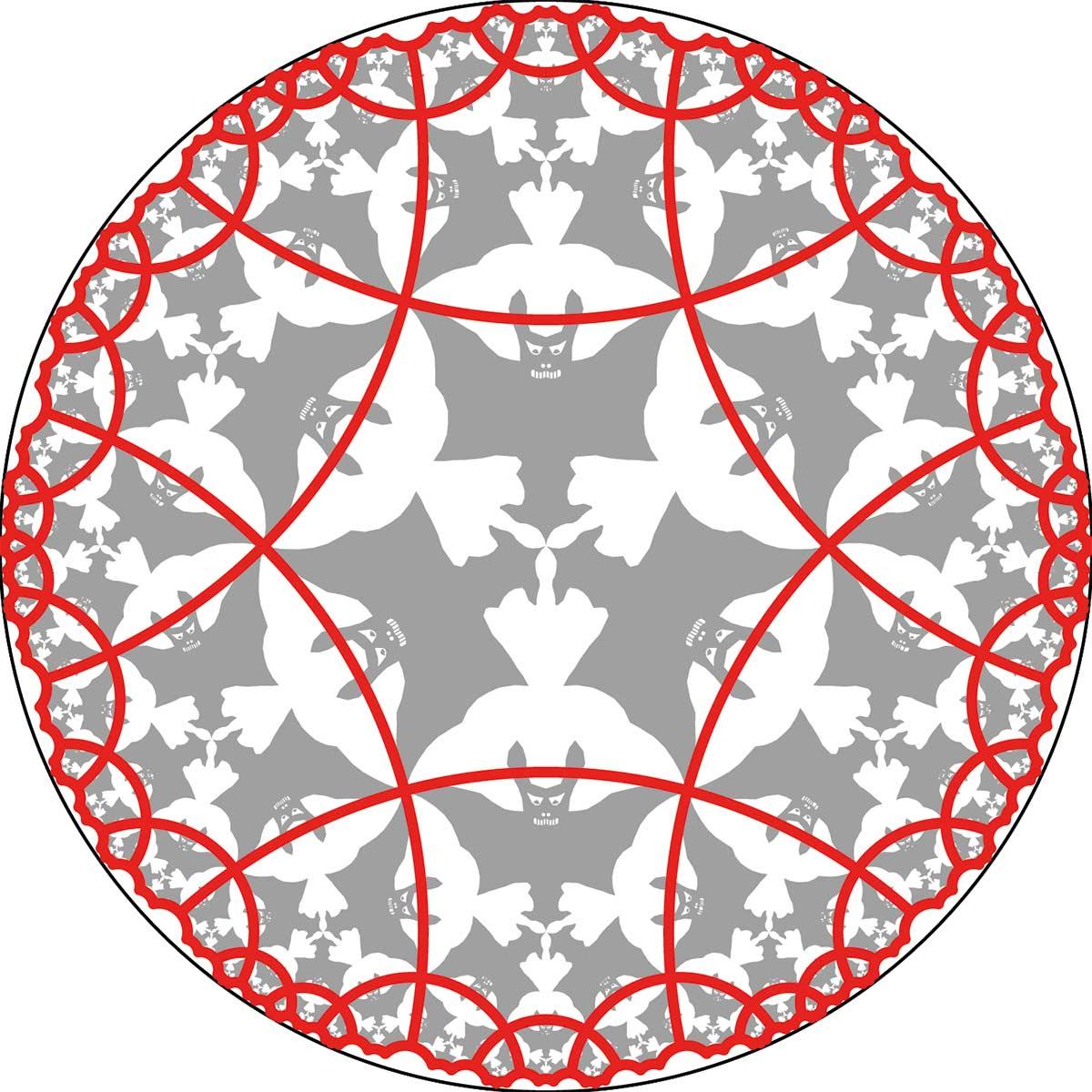
A flurry of correspondence ensued between the graphic artist and the mathematician, with Escher asking for advice on how to proceed with his attempts to master these hyperbolic tilings. Coxeter in turn learned from Escher because the latter came up with solutions for this form that the professor had not yet considered. The mathematical side, however, remained extremely difficult for Escher. In 1960, when he sent the professor a print of Circle Limit III, he received an enthusiastic letter back. But again he did not get the gist of Coxeter’s message:
‘Three pages full of explanations of what I have actually done. Too bad I do not understand any of it—absolutely nothing.’**
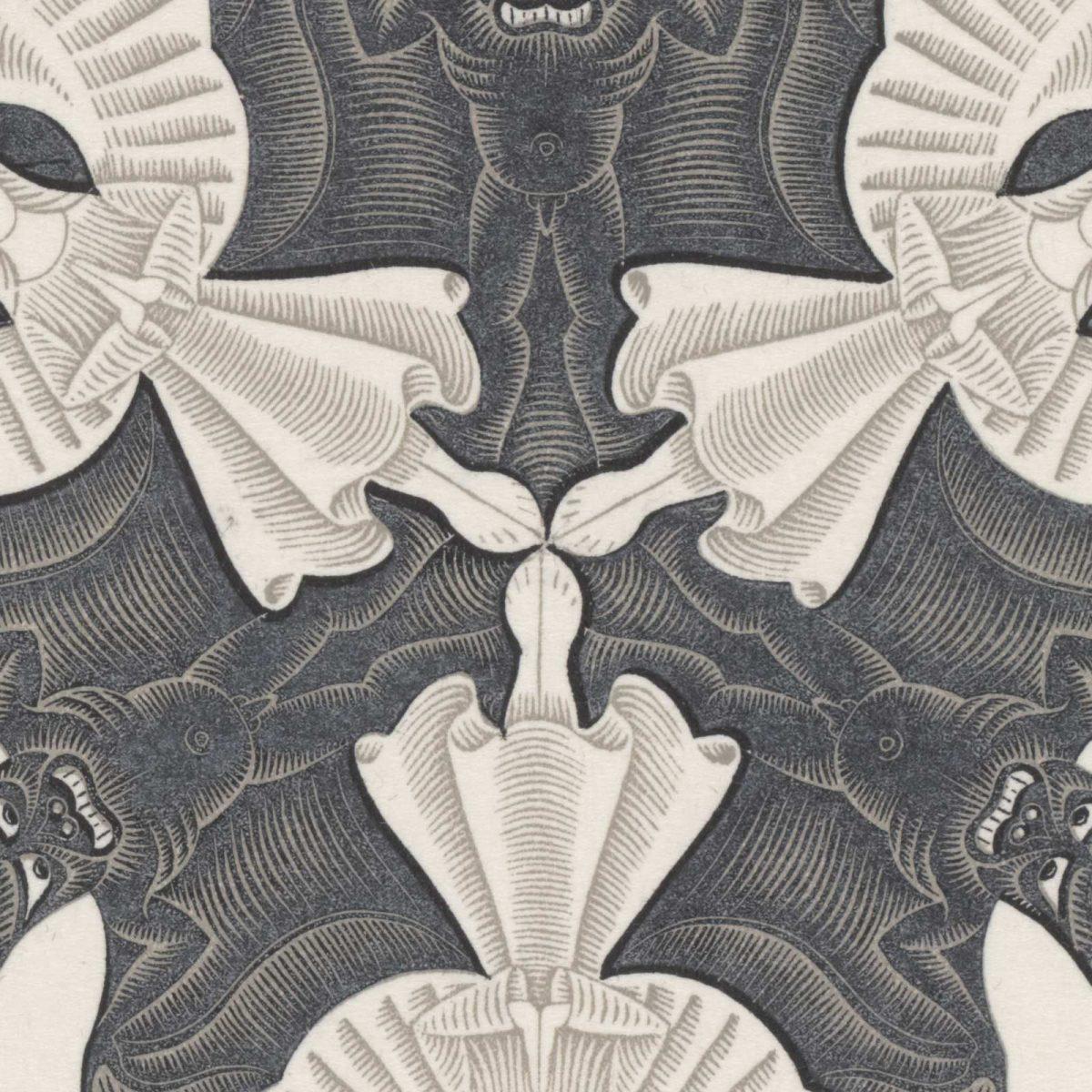
As a basis for Circle Limit IV, Escher used a drawing from one of his sketchbooks: Regular Division drawing no. 45, done during Christmas 1941. The subtitle of Circle Limit IV is ‘Heaven and Hell’. The print presents us with white ‘angels’ and black ‘devils’ (in the form of bats). The three angels and three devils in the middle complement each other perfectly. Good and evil need each other in order to be visible, to infinity.
What is so fascinating and brilliant about Escher is that he succeeded in making hyperbolic tilings based on complex mathematical theories about which many mathematicians have racked their brains, despite the fact that he himself did not understand anything about these theories.
Professor Thomas Wieting wrote a very interesting paper about the development of the circle limits. It’s also available as pdf.
In this video Coxeter brings Escher’s circle limits together with the theory behind them.
Source
[*] and [**] Wim Hazeu, M.C. Escher, Een biografie, Meulenhoff, 1998, page 404-408